D.149 – La Terre ne bouge pas – Partie 5-4
CINQUIÈME PARTIE
(4)
SATELLITES GÉOSYNCHRONES (GÉOSTATIONNAIRES)[1]
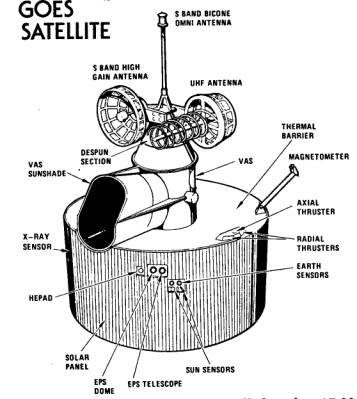
Ces satellites sont différents des quelque 15 000 satellites lancés de la Terre. Tous les autres sont constamment en mouvement au-dessus de la surface terrestre et changent de place à tout moment, d’une minute à l’autre. En moyenne, les autres satellites font le tour de la Terre en 1½ heure.
D’autre part, le soi-disant Satellite Géosynchrone Géostationnaire demeure toujours au-dessus de notre tête en tout temps (un peu comme l’Étoile polaire reste toujours à la même place). Van Nostrand nous offre cette description :
« Un satellite géostationnaire possède une orbite circulaire reposant au niveau de l’équateur de la Terre. Le satellite se déplace autour de l’axe polaire de la Terre dans la même direction et dans la même période de temps que la rotation de la Terre (24 heures). Le satellite reste au-dessus d’un point fixe de l’équateur terrestre. L’altitude d’un satellite géostationnaire est d’à peu près 35 784 km (22 240 mi.] au-dessus de l’équateur. »[2]
On n’a pas à réfléchir longtemps pour s’apercevoir que le phénomène des satellites géosynchrones a directement rapport avec le mouvement ou non de la Terre. Si une couple de douzaines de satellites géosynchrones sont installés en diverses parties du globe et qu’ils demeurent au-dessus de leur site jour et nuit (comme c’est le cas), alors seulement deux explications sont possibles.
L’une de ces explications — la seule qu’on entend ou qu’on lit — est celle qui s’accorde avec l’idée universellement reçue que la Terre tourne sur un axe tous les 24 heures. Cette idée est très joliment résumée dans le nom que l’on donne généralement à ce type de satellite, i.e., « géosynchrones », signifiant qu’ils sont synchronisés à la supposée rotation de la Terre. Comme nous venons de le voir dans l’Encyclopédie Scientifique, ce nom dit que ces satellites orbitent autour de la Terre à une vitesse parfaitement synchronisée à la vitesse que l’on suppose à la rotation de la Terre.
L’autre explication — celle dont on entend jamais parler — est celle qui s’accorde avec les déclarations de la Bible affirmant que la Terre ne bouge pas d’un centimètre. Appelons ce phénomène satellite géostationnaire (qui peut du moins laisser entendre que les satellites sont stationnaires au-dessus d’une Terre stationnaire, comme ils semblent l’être jour et nuit).
Or, l’une des deux est vraie. C’est encore Blanc et Noir. Vérité absolue et mensonge absolu. Aucune relativité, ici. La Terre ne peut pas tourner alors que les satellites demeurent immobiles. Ils ne seraient pas à la même place tout le temps. De la même manière, la Terre ne peut pas demeurer immobile alors que les satellites font orbite autour d’elle. Encore une fois, ils ne seraient pas à la même place tout le temps, n’est-ce pas ?
Par conséquent, comme nous l’avons noté (puisque le fait indiscutable, c’est que ces satellites-là sont à la même place tout le temps), soit que la Terre est en rotation et que les satellites orbitent en synchronisme, ou soit que la Terre est immobile et que ces satellites sont immobiles aussi (un peu comme l’étoile polaire mentionnée plus haut et le Globe en Lévitation que nous avons vu dans l’Illustration XII).
Une des explications exige une Terre qui tourne et accommode le concept héliocentrique. L’autre explication exige une Terre immobile et accommode le concept géocentrique. L’une est vraie, l’autre est fausse. Les deux ne peuvent être vraies et il n’y a pas de troisième explication.
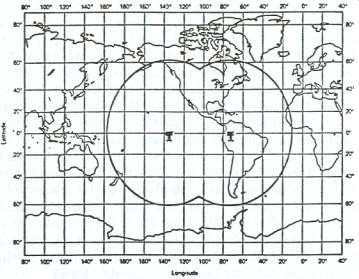
Bien. Prenons maintenant conscience d’une caractéristique pertinente à ces rainures dans l’espace où se tiennent les satellites géostationnaires. Ces « rainures » ont pour caractéristique qu’elles sont très, très loin de la Terre, comparé à la position de tous les autres satellites. La majorité de ces équipements se situent dans un champ variant de 200 à 400 milles [320 à 640 km] d’altitude, certains plus près, d’autres plus loin. Mais ces satellites géostationnaires (desquels nous recevons les photos météo télévisées et desquels nos « soucoupes » satellites reçoivent leurs signaux) sont là-bas à exactement 22 236 milles [35 578 km]. C’est entre 50 à 100 fois plus loin que la moyenne des emplacements satellites. Et cette distance de 22 236 milles est l’unique altitude où fonctionnent ces machins ! Étrange, n’est-ce pas ?
On sent que le Designer y a mis la main. Cela porte quiconque à croire qu’il y a un Designer qui avait prévu que le cerveau de l’homme, qu’Il avait créé, inventerait un jour la télé, les satellites dans l’espace, etc..
Lorsque nous pensons aux vols spatiaux humains partant de Cap Canaveral ou d’ailleurs, nous pensons à une orbite qui atteint généralement de 150 à 250 milles [240 à 400 km] d’altitude. Si vous installez un globe terrestre d’un diamètre d’environ un pied [30 cm] devant vous, en figurant qu’il représente environ 8 000 milles [12 800 km] de diamètre, alors 1½” [4 cm] équivaudra à 1 000 milles. À 250 milles d’altitude, vous regardez la surface à environ ⅜” [3 mm]. Trois huitième de pouce, ou 3 millimètres.
Or, à 22 236 milles [35 578 km], on parle d’une distance de 2 pieds et 9 pouces [83,82 cm] de la surface de votre globe. C’est à peu près neuf fois plus loin. Bien. Maintenant, le premier (et le dernier !) argument presque logique en faveur de ce que les Satellites géostationnaires orbitent, c’est que tous les autres satellites orbitent autour de la Terre, donc, ce type de satellite doit aussi orbiter. Ça semble avoir du bon sens et, puisque que nous avons tous été endoctrinés à croire que la Terre tourne, cette « logique » nous apparaît assez correcte, merci, et nous n’avons plus besoin d’y réfléchir plus avant.
Les critiqueurs nous lanceront : « Eh bien voilà ! Tous les autres font le tour sur leur orbite, alors eux aussi doivent orbiter ! Le fait qu’ils demeurent au même endroit tout le temps signifie que leur propre orbite est synchronisée avec la rotation de la Terre ; donc, ils semblent ne pas bouger. C’est pourtant simple ! »
Nous allons voir ça. Prenons d’abord le point suivant en considération : commençons par calculer la distance de l’orbite supposée des satellites géostationnaires. Nous prenons le rayon de la Terre qui est établi partout comme étant 3 959 milles [6 334,4 km]. Nous ajoutons ensuite la distance séparant la surface terrestre et la « rainure » où opère le satellite géostationnaire. Cela nous fait 22 236 milles [35 578 km] plus 3 959 milles [6 334,4 km] pour un résultat de 26 185 milles [41 896 km]. Puis, nous doublons ce chiffre pour obtenir notre diamètre. Ça donne 52 390 milles [83 824 km]. Ensuite, nous multiplions par pi (3.141592) qui nous montre que la circonférence de l’orbite est de 164 560 milles [263 296 km]. Après cela, si nous divisons ce chiffre par 24 heures, nous constatons que la vitesse à laquelle doit aller le satellite géostationnaire pour demeurer à la même place est de 6 856 MPH [10 969,6 km/h] !
« Ça ne prouve encore rien ! »
C’est vrai. Mais attendez la suite. Nous voulions simplement nous assurer que nous allions tous bien comprendre ce que veut dire affirmer que ces satellites particuliers orbitent autour de l’équateur d’une Terre en rotation. Sa vitesse doit être synchronisée à 6 856 MPH [10 969,6 km/h]. Ici, comprenez bien qu’une simple divergence de ¼ MPH de la vitesse synchronisée écarterait un des satellites d’un mille [1,6 km] à tous les quatre heures. C’est un écart de 42 milles [67,2 km] en une semaine, 180 milles [288 km] en un mois et près de 2 200 milles [3 520 km] en un an. Évidemment, même avec des propulseurs de repositionnement dans le portrait, la moindre divergence ne pourrait être tolérée dans le synchronisme.
« Eh, bien, » répondent les contradicteurs, Nous voyons où vous voulez en venir… Mais cela ne prouve toujours rien, sauf que ces satellites vont très précisément à 6 856 MPH [10 969,6 km/h] en tout temps et demeurent ainsi parfaitement synchronisés avec la rotation de la Terre… »
D’accord, nous avons bien établi cela. Maintenant, superposez cela à l’information que nous avons ramassée jusqu’ici : tous les livres s’accordent à dire que la vitesse de rotation de la Terre n’est pas régulière, égale et stable, mais qu’elle est irrégulière et parfois saccadée et spasmodique. Voici un renseignement à ce sujet :
« Au 19e siècle, la théorie gravitationnelle ne pouvait se rapporter à tous les mouvements observés (de la lune). Or, on pensait parfois que c’était dû à certaines omissions dans la théorie, mais l’on démontra que c’était plutôt dû aux fluctuations de la rotation de la Terre. »[3]
Vous n’aviez peut-être jamais entendu parler de ces irrégularités. Mais vérifiez où vous voulez, vous trouverez la même chose. Vous pouvez donc voir venir ce qui va suivre, n’est-ce pas ? Cela signifie que tout ralentissement ou reprise de vitesse que ferait la Terre devrait être reproduits en parfait synchronisme par le satellite. Et, puisqu’il faut plus de foi pour croire que pareille chose arrive effectivement, jour et nuit, qu’il en faut pour croire que l’homme a été trompé dans toute l’affaire du copernicisme, on en n’est qu’au début du problème de crédibilité… Car il y a plus !
Toutes les « soucoupes » satellites que possèdent des millions de personnes sont atteintes à une variété de points le long d’un grand arc étendu sur plusieurs longitudes. Ces « soucoupes » sont touchées par un satellite à la fois. De nombreux propriétaires captent un seul satellite, laissent leur « soucoupe » dans cette position pendant des années et reçoivent un signal clair. De toute évidence, le satellite ne bouge pas. D’autres propriétaires déplacent leur « soucoupe » d’un satellite à l’autre aussi souvent qu’ils le désirent. Sachant cela, vous, les contradicteurs et autres tenants du copernicisme, ne vous apparaît-il pas illogique que des satellites déployés à des milliers de kilomètres puissent tous ajuster leur vitesse orbitale en coordination avec le constant ralentissement et la reprise de vitesse de la soi-disant rotation de la Terre ?? Cela vous donne-t-il à réfléchir ?
Et pendant que vous réfléchissez à ces problèmes soulevés par les satellites géostationnaires, prenez cet autre en considération… Eh oui, encore ! En fait, chers amis, vous ne pourrez entendre tout ce que nous avons à vous dire à propos des satellites géostationnaires sans finir par savoir que ni eux, ni la Terre ne bougent.
SATELLITES GÉOSYNCHRONES (GÉOSTATIONNAIRES) # 2

Cette illustration dépeint une des découvertes de Kepler. Branley est une autorité en matière d’étude de la lune et des satellites artificiels. Il paraphrase Kepler :
« Les planètes … et la lune se déplacent en orbites elliptiques (…) et une ligne rejoignant la terre à la lune balaierait des superficies égales en des périodes de temps égales. Examinons ce que cela signifie. Dans le diagramme ci-contre, supposons que la lune se trouve en A. Il faut cinq jours à la lune pour se rendre en B. Plus tard, la lune est en C. Il faut cinq jours à la lune pour se rendre en D. Vous remarquerez facilement que AB est plus long que CD. Pourtant, le même laps de temps est requis pour que la lune se déplace de A à B et de C à D ; par conséquent, la lune doit se déplacer plus vite pour franchir la distance séparant A de B. Lorsque la lune se trouve dans la superficie A-B, elle est près de la terre (périgée), elle se déplace donc plus vite. Quand la lune se trouve dans la superficie C-D, elle est loin de la terre (apogée), elle se déplace donc plus lentement. La vitesse doit varier de cette façon parce que Kepler a prouvé qu’une ligne tirée de la terre à la lune doit s’étendre sur des superficies égales en des laps de temps égaux ; en d’autres termes, la superficie 1 doit égaler la superficie 2. »[4]
Or, avec ceci en tête, notez ce qu’en dit encore l’expert de la lune et des satellites, Branley :
« La vélocité de toutes les planètes ainsi que de tous les satellites naturels et artificiels varie de la même manière. »[5]
À partir de ces deux affirmations, nous pouvons d’hors et déjà déceler deux sérieux problèmes à l’encontre du Système copernicien. En fin de compte, les satellites géostationnaires sont certainement artificiellement fabriqués et ils n’obéissent pas à la « loi » de Kepler dans leur soi-disant orbite géosynchrone autour de la Terre. Ici, il y a quelque chose qui se déglingue drôlement ! Ces satellites géostationnaires n’ont pas de périgée et d’apogée ; ils demeurent toujours à la même distance de la Terre ! Cela veut dire que leur orbite supposée ne serait pas elliptique, s’ils se déplaçaient, mais devrait être circulaire. Juste ce simple fait annule le besoin de « balayer des superficies égales » à différentes vitesses.
Apparemment, en tentant de sauver les éléments de cette affirmation képlérienne, on fait face à une réalité qui détruit le copernicisme, c’est-à-dire que les satellites géostationnaires demeurent tout le temps au même endroit, ce qui s’avère une impossibilité si « la vélocité de … tous les satellites naturels et artificiels varie de la même manière, » comme on vient juste de nous l’assurer. En outre, cette réalisation qui détruit le copernicisme devient plus tranchante si l’on essaie d’accorder la soi-disant vitesse de rotation erratique de la Terre aux exigences de Kepler dont Branley nous assure qu’elles s’appliquent à tous les satellites. Tout d’abord, ces satellites ne peuvent en aucune façon aller plus vite, ou plus lentement, pour accommoder Kepler (ou Branley) et demeurer encore stationnaires, comme c’est le cas, à l’évidence. Et même si cette impossibilité était permise, ces vitesses plus ou moins rapides de Kepler devraient elles-mêmes être constamment ajustées pour s’adapter aux supposées vitesses erratiques de rotation de la Terre elle-même. Un tel composé d’impossibilités logiques ne peut être vrai.
Donc, pour une couple de raisons, la « loi » de Kepler n’est pas une loi en ce qui a trait aux satellites géostationnaires. Ce qui revient à dire que les « scientistes » n’ont pas d’explication à fournir quant aux satellites « géosynchrones » pouvant demeurer à la même place tout le temps, pendant que la Terre est supposée ralentir et accélérer en-dessous d’eux. Plus important encore, cela nous démontre que la soi-disant grande contribution que Kepler (le sorcier ?) fit à la véritable science, i.e., que tout exécute une orbite elliptique, n’a jamais été une loi ! Les vraies lois scientifiques (comme la 2e Loi de la thermodynamique et la Loi de la biogenèse, qui nient toute allégation évolutionniste) ne comportent aucune exception.
Or, les satellites géosynchrones géostationnaires, si jamais ils orbitaient, devraient assurément posséder une orbite circulaire, pas une orbite elliptique. L’idée complète du cercle représentant la perfection divine fut censément évacuée par les « lois » de Kepler. Toutefois, ces cercles nous reviennent avec ces satellites parce que la Cosmologie copernicienne exige qu’ils soient sur une orbite circulaire. Ce qui constitue le cercle parfait dessiné par Dieu n’est pas une orbite, mais la fine bande électromagnétique située exactement à 22 236 milles [35 578 km] d’ici, où sont fixés ces satellites dans une position stationnaire relativement à la Terre. La perfection de Dieu, tel que l’exemple de ce cercle, revient à notre époque comme une vengeance, car c’est au moyen de ces satellites captés par cette bande circulaire qu’Il fournit la preuve concluante que le copernicisme est une séduction universelle et que Sa Parole détenait la Vérité pendant tout ce temps !
Il y a encore beaucoup à soutirer de l’exemple des satellites géostationnaires. Vous allez trouver que les trois modes de pensées suivants sont fort ruineux pour le concept héliocentriste.
SATELLITES GÉOSTATIONNAIRES # 3
Réfléchissons ensemble aux rapports météos télévisés. Voici la situation :
- Nous avons les nuages qui se déplacent en direction est à une vitesse de 15 MPH [24 km/h] vers une Cité X. (Souvenez-vous : dans le système copernicien, la Terre tourne vers l’est.)
- « Accroissez » la « rotation de la Terre » sous les nuages de 15 MPH. Mais n’accroissez pas la vitesse des nuages.
- Ça fera en sorte que les nuages sembleront « stationnaires », i.e., synchronisés à la Terre en-dessous. Les nuages n’avanceront plus en direction de la Cité X, comme ils le faisaient avant que la rotation de la Terre ne soit accrue de 15 MPH.
- Nous savons que les vrais nuages, dans le vrai monde, vont continuer à s’avancer vers la Cité X. (Après tout, l’exemple ci-contre n’a qu’une but démonstratif.)
- Néanmoins, deux aspects de l’exemple sont vrais. Seule l’accélération de la Terre a été inventée. Par conséquent, si les nuages se déplacent vers la Cité X — et c’est ce qu’ils font, bien sûr — il ne peut y avoir qu’une seule des trois explications suivantes :
a) Une Terre mobile qui va 15 MPH plus lentement que les nuages et ceux-ci se déplacent vers la Cité X.
b) Les nuages se déplacent 15 MPH plus lentement que la rotation de la Terre à cette latitude (la réponse conventionnelle).
c) La Terre est stationnaire et les nuages se déplacent à 15 MPH vers la Cité X.
Maintenant, la réponse 5a est très intéressante pour deux raisons. La première est qu’on doit l’admettre comme possibilité sous le rapport de la Théorie de la Relativité. C’est vrai parce que, comme nous l’avons vu, la Théorie des Équivalences d’Einstein exige qu’une station ferroviaire puisse aller à 60 MPH [96 km/h] et que le train demeure immobile, que le sol puisse se soulever pour vous frapper la figure lorsque vous tombez, etc., etc.. Donc, vu sous le point de vu des exigences de la Théorie de la Relativité, les nuages de notre exemple pourraient être stationnaires et la Terre s’ajuster à 15 MPH plus lentement…
C’est ça ou alors on tire la Théorie d’Équivalences d’Einstein par la fenêtre avec tout le concept de la Relativité ! On ne peut avoir les deux !
La deuxième chose très intéressante : si l’on persiste à appliquer les Théories des Équivalences et de la Relativité à cette situation, disant que les nuages peuvent être stationnaires et que la Terre puisse tourner en dessous 15 MPH plus lentement afin qu’ils atteignent en temps la Cité X, on détruit alors encore les fumisteries des Équivalences et de la Relativité ! Voici pourquoi : Les nuages se déplacent dans toutes les directions de la boussole, pas juste vers l’est ! Ils se meuvent à des vitesses diverses ! La Terre ne pourrait tourner vers l’est, l’ouest, le sud et le nord en même temps ! Ce serait insensé et Einstein ne pourrait inventer assez de mathématiques pour expliquer cela. De plus, tout ralentissement ou accélération équivalents de la Terre pour s’accorder à la vitesse apparente des nuages feraient en sorte que la Terre révolutionnerait trop vite ou trop lentement pour faire un tour complet en 24 heures, occasionnant le chaos partout.
Si vous comprenez cela, vous voyez que la Relativité d’Einstein s’écrase et que le copernicisme subit une blessure mortelle. Si la Relativité est abattue alors tout le monde s’aperçoit qu’il peut y avoir de la matière inerte dans l’univers et que la Terre pourrait être le plus bel exemple de cette réalité.
Poursuivons avec l’explication 5b qui se trouve piégée avant de commencer… Si l’on croit que le Système copernicien est correct, la conclusion de cette explication ne semble-t-elle pas raisonnable ? Elle SEMBLE raisonnable, et voilà la raison pour laquelle cette réponse s’autodétruit avant de commencer. L’explication « b » est raisonnable si l’on permet le système copernicien. En effet, l’explication « a » est totalement déraisonnable et ne pourrait pas marcher, comme nous venons de le voir, tandis que la réponse « c » est exclue par les coperniciens, donc, « b » est la seule réponse possible pour les coperniciens. Vous me suivez ?
Mais si c’est la seule réponse possible, alors nous devons reprendre conscience que les théories des Équivalences et de la Relativité exigent que 1) tout soit en mouvement, 2) personne ne puisse dire ce qui bouge par rapport à l’autre.
Ainsi, les héliocentristes ne peuvent jamais déclarer catégoriquement que « b » est vérité en la matière sans esquiver le problème des Équivalences et de la Relativité. Et cela signifie que s’effiloche tout le tissu d’hypothèses « scientifiques » fabriqué depuis l’affaire Michelson-Morley. Et, en retour, cela se résume à admettre que l’immobilité est possible et que, finalement, il y a un éther immobile et une Terre immobile. En fait c’est l’exemple classique du dilemme à doubles cornes. La réponse « b » est évidemment la seule avenue raisonnable ouverte aux héliocentristes, mais ils ne peuvent lui donner leur aval inconditionnel, car ils doivent alors admettre que la réponse « a » constitue une option tout aussi valable, même s’ils savent au fond d’eux-mêmes que c’est totalement déraisonnable et, en outre, impossible.
De l’autre côté du tableau, les géocentristes bibliques ne font face à aucun dilemme de la sorte. Leur position s’accorde avec tous les faits connus. Ils n’ont pas à se battre contre toute une liste d’absurdités illogiques coiffées de l’exigence que la Terre et son imperturbable atmosphère se promènent dans l’espace dans quatre directions différentes et à des vitesses dépassant 250 fois celle d’une balle de fusil. En vérité, l’argument géocentrique de la Bible est un modèle de simplicité et de certitude logique comparé au modèle copernicien.
Pourtant, nous devons comprendre que les coperniciens n’ont d’autre choix que de conclure que l’atmosphère tourne avec la planète[6] comme s’il y était collé. Car si la Terre tournait, l’atmosphère devrait tourner avec elle ou alors l’héliocentrisme se transforme en ballon qu’un enfant de dix ans peut crever facilement. Une Terre tournant à l’intérieur d’un atmosphère immobile rappellerait immédiatement la question des avions allant d’est en ouest.
Ceux qui vont vers l’est seraient difficilement capables de se maintenir au niveau de la rotation de la Terre, alors que ceux prenant la direction ouest se rendraient à destination à la vitesse de l’éclair. En fait, l’on n’aurait qu’à monter dans un hélicoptère dans une localité à l’est, flotter un peu dans l’air et atterrir ensuite dans une localité à l’ouest. Même lancer une flèche bien droit dans l’air révélerait très rapidement l’absurdité de ce modèle.
Donc, les héliocentristes n’ont pas le moindre choix, dans ce concept. Il est d’une inévitable nécessité absolue pour les héliocentristes d’avoir une « enveloppe atmosphérique » qui tourne avec la Terre (et qui file et qui glisse à toute allure aux vitesses que l’on suppose) sans en être le moindrement affectée.
Encore là, les géocentristes n’ont pas à résoudre d’aussi absurdes énigmes. La Terre est figée, l’atmosphère se déplace un peu dans toutes les directions, comme n’importe qui peut le voir, le sentir, l’entendre. C’est ainsi. Comment cela cadre-t-il avec la température ? En tête de liste des illogiques absurdités observables concernant le mouvement des nuages que les héliocentristes doivent adopter, il y a le comble des rapports provenant des satellites géostationnaires. Dans ces rapports, nous sommes témoins des mouvements accélérés des nuages dans le contexte d’une Terre qui ne bouge pas. Les héliocentristes disent qu’ils peuvent résoudre le problème, ainsi que celui des avions allant d’est en ouest, etc., avec la réponse « b ». Ils sont en sécurité… pensent-ils.
Mais nous allons récuser le droit aux héliocentristes de se réfugier dans la réponse « b ». Les héliocentristes modernes sont relativistes et nous devons insister pour qu’ils ne puissent esquiver la trappe que leur posent les rapports météos télévisés, mais qu’ils aient plutôt à faire face à la dénonciation de leur théorie absurde en appliquant celle-ci aux exemples très nets que nous observons journellement sur nos téléviseurs.
Nous les forçons ainsi à admettre que la réponse « a » est d’une possibilité égale à la réponse « b ». Dans la réponse « a », les nuages atteignent la Cité X en temps parce que la Terre ralentit de 15 MPH [24 km/h] pour le permettre… mais tous les autres nuages allant dans toutes les autres directions à différentes vitesses ne finiront pas par atteindre géographiquement les mêmes endroits où les envoie le météorologue en un laps de temps de quelques secondes ! C’est impossible ! Pourtant, les images satellites géostationnaires ne mentent pas. Les nuages vont effectivement de A à B, partout sur le globe, lors des séquences de 10, 20 ou 30 heures. C’est une preuve certaine et positive, observable et vérifiable, que la réponse « a », avec toutes les absurdités einsteiniennes à propos des Équivalences construites dessus, n’est qu’une ineptie longuement distillée.
Et sans cette folle idée d’Équivalences, tout le concept de Relativité tombe en morceaux. Or, n’oublions surtout pas que c’est la Relativité qui a permis aux « scientistes » de se sauver de « l’inacceptable » conclusion de l’expérience Michelson-Morley…
Alors les images météos des satellites géostationnaires obligeraient-elles donc l’establishment scientifique à se rendre compte qu’il est retourné à la case départ en ce qui a trait aux résultats de l’expérience Michelson-Morley ? Précisément. Ces images météos télévisées balaient plus d’un siècle de sauvages efforts pour contourner les résultats de cette expérience. Nous avons vu quelle transpiration et quelles pressions ils leur occasionnèrent et comment Einstein et sa Relativité sauvèrent les meubles. Or, si la Relativité est tout ce qui compte, nous avons parfaitement le droit de pousser les relativistes à jouer selon leurs propres règles en matière de météo télévisée. Et une fois qu’ils jouent selon ces règles, le mensonge du siècle est exposé devant tous.
En ce qui a trait à la fameuse réponse « b », en reste-t-il quelque chose ? La seule chose qui ait marché en sa faveur, c’était l’apparente impossibilité pour quiconque d’être capable de réfuter sa déclaration que « l’enveloppe atmosphérique » était collée à la Terre et que, non seulement tournait-elle avec la Terre, mais qu’elle n’était pas du tout dérangée par les diverses vitesses allant d’un millier à un demi-million de milles à l’heure. C’était à la limite du non-sens, bien entendu, mais il ne semblait y avoir aucun moyen de la désapprouver.
Or, il y a aujourd’hui un moyen. Grâce à la dénonciation du non-sens de la Relativité par les images satellites météorologiques télévisuelles, nous revenons à l’éther dont les scientistes avaient accepté l’existence avant qu’Einstein la déclare inexistante sur son tableau noir. Vous vous rappelez ?
Alors voici : tout le monde acceptait un éther depuis Copernic en passant par Maxwell jusqu’à Michelson-Morley, parce que les scientistes n’avaient qu’à dire que l’atmosphère tournait avec la Terre sans craindre que qui que ce soit prouve qu’ils avaient tort. Mais les résultats de l’expérience Michelson-Morley révéla l’immobilité de la Terre de DEUX manières. Et les deux étaient reliées à l’orbite annuelle supposée de la Terre autour du soleil en une distance de 585 000 000 milles [936 000 000 km]. Dans le premier cas, les ondes lumineuses auraient dû être dans l’autre sens lors de l’expérience conduite six mois plus tard ; mais elles ne le furent pas. Pour ce qui est de l’autre chose, la soi-disant vitesse orbitale de plus de 66 000 MPH [105 600 km/h] aurait dû donner une impulsion de départ à la lumière dans l’un des bras métalliques de l’interféromètre, mais ce ne fut pas le cas non plus. Ces deux résultats donnaient la preuve nette que la Terre ne bouge pas.
D’une manière ou d’une autre, l’éther devait disparaître, mais aucun des « scientistes » n’avait réussi, jusqu’à Einstein, à s’en débarrasser. Alors, Albert arriva avec sa baguette magique de Relativité…
L’éther devait disparaître pour deux raisons : 1) elle était apparemment immobile et l’idée que quelque chose puisse être immobile dans l’univers amenait la conclusion que la Terre pouvait l’être aussi. Mais vous vous rappellerez que Engles et d’autres matérialistes avaient déjà déclaré que rien dans l’univers ne pouvait être immobile. 2) L’éther pouvait créer de la friction avec la Terre filant au-travers d’elle à plusieurs vitesses atteignant jusqu’à un demi-million de milles à l’heure. Ce qui pouvait faire exploser l’atmosphère.
Or, tout cela était fort bien compris et accepté avant l’expérience Michelson-Morley. Mais cela se transforma soudainement en facteur critique lorsque la lumière traversant l’interféromètre ne démontra aucun mouvement de la Terre. Cela fit apparaître plus largement les questions concernant l’éther et menaça davantage le copernicisme. L’expérience avec la vitesse de la lumière disait que la Terre ne bouge pas, donc, que l’atmosphère autour d’elle ne se déplace pas au-travers de l’éther, exactement comme le stipule la Bible, Brahe et tous les autres géocentristes.
C’est alors que FitzGerald, Lorentz et, en fin de compte, Einstein se débarrassèrent de l’éther et établirent que la vitesse de la lumière était toujours indépendante de la source de laquelle elle émanait.
De là, on en arrive à trois choses : 1) les rapports météos télévisés exposent et détruisent la Relativité einsteinienne et toutes les absurdités qui reposent sur elle. 2) Cette dénonciation ramène les sciences de l’astrophysique, de l’astronomie et de la cosmologie à leur point de départ, lorsque les expériences Michelson-Morley des années 1880 démontrèrent, de façon répétitive, que la Terre ne tourne pas. 3) Cette fois, grâce aux images des satellites géostationnaires, toute échappatoire par le moyen du Relativisme démentiel est coupée et l’establishment « scientifique » doit réfléchir à « l’impensable ».
Trois hourras pour les Satellites géostationnaires ! Et il y a encore d’autres manières que ces lascars peuvent démontrer que la Terre ne bouge pas ! L’establishment « scientifique » s’est vraiment tiré dans le pied en inventant ces bébés ! En fait, pas dans le pied… dans la tête !
SATELLITES GÉOSYNCHRONES GÉOSTATIONNAIRES # 4


Étrange que ces satellites géostationnaires se tiennent exactement à 22 236 milles [35 578 km] et nulle part ailleurs… mais pas aussi étrange dans le système géocentrique que dans le système héliocentrique. Prenons ceci en considération : la « science » a volontiers fait reposer son cas d’une Terre qui tourne sur le « Pendule » de Foucault, n’est-ce pas ? Bien. Souvenez-vous maintenant que ce « Pendule » se maintient « dans un endroit fixe dans l’espace », selon toute la littérature le concernant. Immobile, comme tout le monde peut voir, le bidule est incontestablement maintenu au plafond attaché aux murs attachés au plancher d’un building qui est attaché à la Terre. Si la Terre tournait, partout où elle irait, elle emmènerait l’arrimage où est accroché le « Pendule » de manière aussi assurée qu’elle emmènerait le plafond, les murs, le plancher, peu importe le genre d’instrument pivotant qui le maintient.
Endroit fixe, mon œil ! Mais c’est pourtant ce que l’on considère dans le monde entier. Remarquez de quelle manière Umberto Eco fait ressortir ce concept dans sa récente nouvelle Le Pendule de Foucault :
« Et quand, l’an dernier, je vis le Pendule de Foucault, je compris tout. »
Tout ?
« Presque tout. Tu vois, Casaubon, même le Pendule est un faux prophète. Tu le regardes, tu crois que c’est le seul point fixe dans le cosmos, mais si tu le détaches du plafond du Conservatoire et que tu le pends dans un bordel, il fonctionne pareillement. Et il y a d’autres pendules ; il y en a un à New York, dans le building de l’ONU ; il y en a un dans le musée des sciences de San Francisco, et Dieu seul sait dans combien d’autres endroits. Où que tu l’installes, le Pendule de Foucault se balance à partir d’un point fixe pendant que la Terre tourne sous lui. Tous les points de l’Univers sont des points fixes : tout ce que tu as à faire, c’est d’y amener un Pendule. »[7]
Alors, voyez-vous, le concept d’un « point fixe », i.e., un endroit ou un poste immobile dans l’univers est, dit-on, n’importe quel lieu où se balance un Pendule de Foucault du haut d’un plafond et maintenu par un joint pivotant. La « sagesse » de l’homme a accepté et établi ce point fixe bidon et a trompé la multitude avec. N’est-il pas vraiment intéressant de voir que certains « points fixes dans l’univers » sont, non seulement jugés possibles, mais également un concept absolument nécessaire de la fameuse démonstration de Foucault qui était destinée à persuader l’humanité que la Terre tourne ?
Qu’y aurait-il d’étrange, alors, qu’il y ait un vrai « point fixe » à la disposition de l’homme démontrant hors de tout doute que la Terre ne bouge pas ?! Nous avons vu l’illustration d’une démonstration du champ électromagnétique qui maintenait immobile en l’air un « Globe terrestre en lévitation », n’est-ce pas ? Le fait même que les satellites géostationnaires ne fonctionnent qu’à une altitude bien précise au-dessus de l’équateur et que cette altitude ne varie jamais — comme le font tous les autres satellites — est virtuellement une preuve en elle-même que ces satellites sont pris dans une bande étroite circulaire, un champ magnétique qui produit le même effet que l’on peut observer avec le « Globe terrestre en lévitation »
Quel fait étrange qu’il y ait une plage précise dans le ciel, à 22 236 milles [35 577,6 km] en dehors de la Terre où ces satellites géostationnaires peuvent être installés dans un champ magnétique qui les maintient en place, sans crochet, sans plafond, sans murs, sans plancher ! Et comme c’est étrange, comparé aux bidules du Pendule de Foucault, que l’œil d’une légère caméra agisse sans frottement alors que son câble sort du satellite et capte en-dessous la variation des nuages de la Terre et son système de température ! Un peu comme si les nuages agissaient comme des poids pendus au bout de la tige d’un pendule se déplaçant ici et là.
Donc, à partir de leur « point fixe dans l’espace », les caméras des satellites nous montrent que les nuages se déplacent un peu partout, mais elles ne montrent jamais la Terre se déplaçant sous elles, même un petit peu (alors encore bien moins à des vitesses de centaines et de milliers de milles), pendant les quelques heures d’exposition.
Tout le monde peut arriver à comprendre comment le satellite ne peut bouger, coincé qu’il est dans le champs magnétique. Or, les illustrations météos nous indiquent que la Terre ne peut pas bouger , car ce « point fixe » magnétique dans l’espace révèle de façon claire des nuages qui se déplacent et des systèmes de tempêtes, mais ne démontre aucun mouvement de la part de la Terre elle-même.
Ce que nous pouvons donc voir de plus en plus, c’est qu’il y a une PREUVE visuelle solide et indiscutable, tout autour de nous, de ce que la Terre ne tourne pas. Le Gros Bluff du copernicisme fut condamné à la dénonciation dès lors que les satellites géostationnaires ont commencé à fonctionner. Ce n’était qu’une question de temps. Ces preuves ordinaires nous offrent un témoignage de la profondeur et de l’étendue de l’endoctrinement du monde dans la contrefaçon héliocentrique jusqu’à aujourd’hui ! Pourtant, chaque parcelle de preuve est contre le mouvement de la Terre ; toutes les preuves ! Ils n’ont rien de leur côté et il est plus que temps que les gens le sachent !
Mais combien de gens dans le monde, pensez-vous, seront heureux de voir l’héliocentrisme exposé en tant que pur mensonge… ?
SATELLITES GÉOSYNCHRONES (GÉOSTATIONNAIRES) # 5
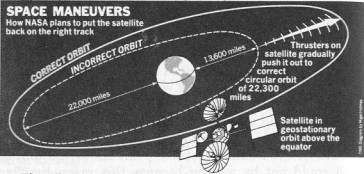
Il y a encore un point concernant ces satellites que nous devons enfoncer avec un piquet de rail de chemin de fer. Il nous faut réaliser et comprendre parfaitement que ces merveilleux satellites sont occasionnellement déplacés par contrôle à distance à partir de la Terre. Quand on les déplace, la vitesse du mouvement est connue et contrôlée d’une manière très précise (dans la lettre ci-après, on cite les chiffres de 16.06 milles [28,6 km] par jour et 0.66 MPH [1,056 km/h]). L’argument décisif — comme le montre clairement la lettre du Bureau des opérations satellites — est celui-ci : tous ces mouvements sont planifiés et exécutés sur la base d’une TERRE FIXE ! Voyez la lettre envoyée par notre spécialiste, Marshall Hall (particulièrement le paragraphe final), dans l’Illustration XVIII. Ensuite, jetez un coup d’œil sur la réponse officielle (aux parties A et B, spécialement), en Illustration XIX. Cette réponse nous donne une information tout à fait pertinente au sujet de la question d’une Terre qui tourne.
Comme vous le voyez, ils disent maladroitement que cette manœuvre de repositionnement d’un satellite géostationnaire est exécutée sur la prémisse que la Terre ne tourne pas ! C’est fort ! Et cette flagrante admission que la manœuvre délicate est calculée et exécutée sur la base d’une Terre immobile, i.e., une « Terre fixe », est de la plus haute importance pour la dénonciation du mensonge copernicien. Ce que cela signifie, en mots clairs et simples, c’est ceci : En ce qui concerne la manœuvre de repositionnement, il n’y a pas de Système copernicien. Point à la ligne. Par conséquent, cette manœuvre est planifiée et exécutée d’après le Système biblique établissant une Terre immobile. C’est un fait !
Si la Terre est « fixe », cela veut dire que le satellite doit aussi se tenir immobile. C’est assurément le cas. Réfléchissez-y. Tout le système copernicien dépend de satellites se déplaçant à près de 7 000 MPH [11 200 km/h] au-dessus d’une Terre tournant à plus de 1 000 MPH [1 600 km/h] au niveau de l’Équateur ! Si le mouvement de la Terre devient FIXE (comme c’est indéniablement le cas par les calculs faits pour repositionner ce type de satellites), alors le satellite doit aussi être arrêté ! S’il n’était pas stoppé, et s’il continuait à voyager à près de 7 000 MPH, il dépasserait le 97,45º de longitude ouest en une fraction de seconde ! Il faut donc qu’il soit arrêté et tenu pour fixe, comme la Terre est tenue pour fixe afin de faire les calculs qui assureront le succès de la manœuvre.
Alors, je vous pose la question : comment stoppe-t-on un satellite qui doit absolument aller à près de 7 000 MPH pour que le Système copernicien se tienne ? Le stoppe-t-on mathématiquement ?? Si on le fait et que l’on est copernicien, ne sait-on pas que nos mathématiques sont fausses parce que l’on « sait » que la chose va effectivement à près de 7 000 MPH ?
|
Traduction de la lettre XVIII 17 novembre 1989 Département du Commerce des Etats-Unis NOAA a/s Charles E. Liddick Chef de la Division des Horaires Bureau des opérations satellites Washington DC 20233
Cher M. Liddick,
Tous mes remerciements pour votre prompte réponse approfondie à mes questions précédentes (une copie de votre lettre ci-attachée). Les trois déclarations suivantes — déduites de votre réponse — sont-elles plus ou moins exactes ?
Concernant le #2, la distance de c. 742 milles de la Terre serait-elle aussi vraie pour le parcourt orbital à 22 300 milles ? En d’autres mots, si le satellite était déplacé sur la surface terrestre du 97,25º O. au 108º O., il serait déplacé de 10,75º ou de 741.75 milles. (Et si on le déplaçait à vitesse constante, cette vitesse serait de c. 17.25 MPH.) De la même manière, sur la lancée du parcourt orbital du satellite de c. 165,217 milles et son déplacement de 97,25º à 108º, la distance parcourue serait la même, n’est-ce pas ? (et la vitesse, si elle est constante, serait la même ?) Sur la base de ces affirmations, mes questions sont :
Merci pour votre aide, Sincèrement, (signature) Marshall Hall
|
Traduction de la lettre XIX 22 novembre 1989
12, Morningside Drive Cornelia, Georgia 30531
Cher M. Hall,
Concernant le #2 : 674,4 milles établis de la terre est la vraie distance aussi pour le parcourt orbital à 22 237 milles établis. En d’autres termes, si l’engin spatial était déplacé sur la surface terrestre de 97,45º à 108º ouest, on le bougerait de 9,75º ou 674,41 milles établis (16,06 milles par jours ou 0,669 MPH).
Sur la lancée du parcourt orbital de l’engin spatial de 164,264 milles établis, et le déplacement du 97,45º au 107,2º ouest, la distance sera la même, à peu près constante.
Sincèrement, (signature) Lee Ranne Navigation GOES/POLAR Bureau des opérations satellites (301) 763-7573
|
En d’autres termes, le satellite doit tourner dans l’esprit des scientistes coperniciens sinon toute la structure copernicienne tombe, et cela constitue une alternative « impensable ». Donc, il doit tourner dans l’esprit des scientistes pendant qu’ils effectuent leurs calculs pour repositionner l’instrument.
Mais voilà que ces scientistes réalisent maintenant que ces satellites allant à près de 7 000 MPH dans le système copernicien doivent être stoppés mathématiquement afin qu’ils puissent faire les calculs qui provoqueront un repositionnement couronné de succès. Or, ces calculs marcheront et aucun autre. Toute la manœuvre délicate fonctionnera parce que les calculs auront été basés sur une Terre et un satellite qui sont immobiles.
Bon, maintenant, cette série de circonstances nous met en face de la proposition que les mathématiques décrivant un satellite immobile au-dessus d’une Terre fixe fonctionnent avec précision et permettent à toute l’opération d’être exécutée dans le monde réel, alors qu’en même temps, ces calculs sont « reconnus » pour être faux par tous les scientistes coperniciens qui les utilisent. Vous saisissez ?
Ils emploient des maths basées sur une Terre immobile parce qu’ils le doivent. Mais ces maths fonctionnent ! Elles ne fonctionneraient pas et ne pourraient fonctionner si le machin voyageait à près de 7 000 MPH, alors ce qu’ils appelleraient de vraies maths représentant une situation véritable ne fonctionnerait pas et ce qu’ils appellent de fausses maths fondées sur une fausse situation fonctionnent. Vraiment étrange…
Donc, l’impasse logique dans laquelle se met le copernicisme, c’est la réalisation que ce qu’un scientiste copernicien doit reconnaître comme de « fausses » maths en faveur d’une Terre fixe et d’un satellite fixe rendent néanmoins possible une manœuvre délicate et précise dans le monde réel (pas en théorie !), et que les « vraies » maths en faveur d’une Terre qui tourne et d’un satellite qui orbite ne permettront pas que la manœuvre fonctionne dans le monde réel.
Nous en avons passablement dit sur les mathématiques bidon et de ce qu’elles sont les seules « preuves » qui soutiennent le mythe copernicien. Toutefois, non seulement les VRAIES mathématiques existent-elles dans le monde réel de la Science appliquée, mais elles sont les seules à faire construire les ponts, les jets et les ordinateurs ; les seules à faire marcher les trains et à mettre les satellites là où ils doivent être. Vu l’utilisation de toute la fausse science des mathématiques bidon dans l’émergence et le succès du copernicisme, ce n’est que justice et parfaite ironie qu’une FAILLE capable de faire basculer la contrefaçon copernicienne se trouve dans cette opération de déplacement satellite très peu connue. Nous voyons ici très clairement que seules les vraies mathématiques peuvent fournir les calculs nécessaires pour accomplir cette action réelle dans le monde réel.
Mais, à l’instant même où cette opération de repositionnement identifie les Vraies Mathématiques, elle révèle également le dur fait que les fausses mathématiques ne fonctionnent que pour de fausses hypothèses qui ne peuvent être testées !
Donc, les vraies mathématiques, fondées sur une TERRE FIXE ET UN SATELLITE FIXE sont les SEULES mathématiques qui assureront le déplacement de ce satellite dans le monde réel. C’est la seule et véritable raison pour laquelle cette opération est basée sur une Terre fixe et biblique ! Ce Système biblique constitue la Vérité et seules des maths fondées sur cette Vérité déplaceront ces satellites de A à B ! Les gens des Opérations Satellites n’utilisent pas une Terre fixe dans leurs calculs parce que c’est plus facile et plus commode que d’employer des calculs basés sur le système copernicien ; ils utilisent les calculs d’une terre fixe parce que ce sont les SEULS qui feront le travail !! Ils n’ont pas le choix, ils doivent employer la Terre fixe !
Pour résumer tout ça, lorsqu’on commanda au Satellite GEOS-7 de se déplacer ¼º vers l’ouest par jour pendant 42 jours, il se déplaça à partir d’une position stationnaire. Et la même chose arriva lorsqu’on le retourna à sa position en est. Et le tout fonctionna ! Les deux repositionnements fonctionnèrent parce que le satellite est maintenu en place dans la bande électromagnétique circulaire et qu’il demeure aussi immobile qu’une statue dans un désert, n’allant nulle part, à vitesse zéro, tant qu’on ne lui donne pas instruction de se déplacer.
Et s’il ne bouge pas, la Terre ne bouge pas non plus…
Et cela veut dire qu’il est temps de revenir à la Bible !
| Nota bene : Une lecture attentive des deux paragraphes suivant le #3 dans la réponse de la NASA du 22 novembre 1989 révèlera une erreur manifeste dans la résolution de la vitesse et de la distance. Cette erreur n’est pas pertinente à ce qui a été dit jusqu’ici, en ce qui me concerne, mais elle mérite néanmoins d’être notée. Selon toute évidence, la distance d’une longitude à une autre ne peut être la même dans un cercle de 165 100 milles [264 160 km] qu’elle l’est dans un cercle de 25 000 milles [40 000 km]. Non plus qu’un trajet de 42 jours aux vitesses données amèneront le satellite de 97,45º de longitude ouest à 107,2 de longitude ouest ! En fait, le satellite doit être déplacé d’environ 4 449 milles [7 118,4 km] à 4,41 MPH [7 km/h] pendant 42 jours pour atteindre sa destination. |
___________________________________________________________________________
[1] La distinction conventionnelle entre satellites géosynchrones et géostationnaires s’établit ainsi : « Un satellite géostationnaire possède une orbite circulaire reposant au niveau de l’équateur de la Terre (…) Le satellite géosynchrone est celui qui orbite autour du centre de la Terre en un cercle exactement synchronisé avec la rotation de la Terre, bien qu’il ne lui soit pas nécessaire d’être sur le plan équatorial (…) Une orbite stationnaire doit être synchronisée, mais une orbite synchronisée n’a pas besoin d’être stationnaire… » [Encyclopédie scientifique Van Nostrand, 7e édition, 1989, p. 2501].
[2] Encyclopédie scientifique Van Nostrand, 7e édition, (Van Nostrand Reinhold, N.Y., 1989), p. 2501
[3] Encyclopédie Britannica, Macropaedia, Interprétations des petites irrégularités du mouvement, Vol. 12, p. 417.
[4] Branley, La lune, p. 22.
[5] Ibidem, p. 23.
[6] Le mot « planète » signifie « vagabond ». Si la Terre ne bouge pas, elle ne vagabonde donc pas et elle n’est pas une « planète » ; ce mot n’est qu’un autre maillon de la longue chaîne d’endoctrinement séducteur destiné à implanter le concept de l’héliocentrisme dans l’esprit des gens.
[7] Umberto Eco, Le pendule de Foucault, (Harcourt Brace Jovanovich, éd., San Diego, N.Y., Londres, 1989), p. 237.

